 Contact: Contact:
Prof. Sethu Vijayakumar
Institute of Perception, Action & Behavior,
University of Edinburgh,
JCMB 2107F, The King's Buildings, Mayfield Road,
Edinburgh EH9 3JZ.
Ph: +44 (0)131 651 3444 (dial-in). Internal: 513444
Fax: +44 (0)131 651 3435
Email: sethu.vijayakumar(at)ed.ac.uk
Tasks:
» Member of the scientific board
» Responsible for Modules 2 and 5
» Basic research in the areas of statistical machine learning, motor control, supervised learning in connectionist models and computational neuroscience
Locally Weighted Projection Regression
Locally Weighted Projection Regression (LWPR) is a recent algorithm that achieves nonlinear function approximation in high dimensional spaces with redundant and irrelevant input dimensions. At its core, it uses locally linear models, spanned by a small number of univariate regressions in selected directions in input space. A locally weighted variant of Partial Least Squares (PLS) is employed for doing the dimensionality reduction.
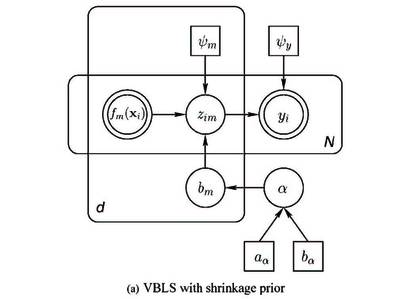 - Graphical model of VBLS with shrinkage prior
Learning the sensorimotor structure in high dimensions
The ability to learn sensorimotor structures is a key to compliant control of robots in a wide range of environments or tasks. Using learning, inaccurate and un-modelled components of analytical model based dynamics can be compensated for, and furthermore the learnt mappings can include sensory inputs such as haptic data, possibly yielding complex but useful sensorimotor contingencies automatically. The application of learning in control however poses special requirements to the algorithms, in particular with respect to computational efficiency, the ability to handle high dimensional data, and the facility to train models in an online, incremental fashion.
Furthermore, adopting an engineering attitude we can explore biologically plausible approaches to study strategies that biological systems might have developed to address these issues.
Within WP2, learning is studied mainly from the following three viewpoints:
1) We developed statistical machine learning approaches that meet the aforementioned requirements.
2) We looked at automatic methods of extracting low dimensional structure from data
3) We studied where and how to integrate learnt models in a control loop, e.g., in feedforward or recurrent architectures.
UEDIN has produced a new implementation of the online learning algorithm Locally Weighted Projection Regression (LWPR). While the algorithm itself had already been proven to be suitable for learning high-dimensional function mappings, previous implementations were either slow (written in pure MATLAB) or rather inconvenient to use. The new implementation uses an efficient low-level core library written in C, but it provides bindings and wrappers for usage from C++, MATLAB/Octave, and Python on multiple platforms, thus making its integration into existing software environments (e.g., the simulator developed at DLR) much easier. The software package, together with documentation and tutorials, has been has been made publicly available, and an accompanying paper has been published in the JMLR track on machine learning open source software. UEDIN has also set up a website for the LWPR implementation, where the documentation and tutorials can be browsed online (http://wcms.inf.ed.ac.uk/ipab/slmc/research/software).
Further, in response to the open question of automatic selection of local complexity parameter in non-linear regression, UEDIN has explored automatic selection of kernel width and dimensionality of local models (Ting, J., D'Souza, A., Vijayakumar, S., and Schaal, S. (2010). Efficient Learning and Feature Selection in High-Dimensional Regression, Neural Computation, vol. 22, no. 4, pp. 831-886) with a potential to scale to high dimensional problems.
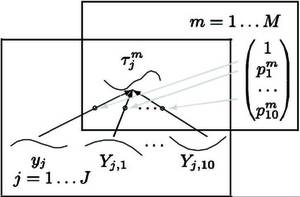 - Multi-task GP model
Managing sensorimotor structures in multiple contexts
At UEDIN, we have extended our methods to incorporate analytical properties of dynamics contexts into learning algorithms. In particular, we investigated how to learn
the inverse dynamics mapping of a robot arm for multiple loads using a single multi-task Gaussian Process regression model. The new multi-task GP approach now explicitly exploits the fact that the underlying nonlinearities Z(\x85) are the same for all contexts, and models the torques with a single covariance function that factorises in the same way as the Z*r decomposition above. Therefore, all training data from all contexts can be collected in a single model, and uncertainty can be shared amongst the contexts. Indeed, since the multi-task GP model learns the decomposition, it can successfully predict the torques for combinations of contexts and input space locations that have not been present in the training data, outperforming interpolation between separately learned single-task models (K.M. Chai, C.K.I. Williams, S. Klanke, and S. Vijayakumar, NIPS 2008).
 - Demonstration of the tactile sensors mounted on Schunk dexterous hand SDH-2.
Active Learning for optimal Sensorimotor Discrimination
The last major subtopic within WP2 is about finding effective ways of generating
exploratory movements, that is, we wish to create movement plans which not just
represent a path between two points A and B, but rather yield informative sensor input during the motion. Working towards this goal involves studying
1) dimensionality reduction of movement data, for representing sequences of postures of systems with possibly large degrees of freedom in a compact manner,
2) dynamical systems representations of movement plans, for being able to flexibly
scale movements in space and time,
3) the optimality of movements with respect to the amount of information they yield, for example in a haptic discrimination task, and
4) dimensionality reduction of sensory data, for acquiring a compact description of what is being sensed, ideally yielding \x93cognitive\x94 notions about the environment.
We have generated novel results in each of these domains. UEDIN has investigated representations of movements which are beneficial for the learning and execution of explorative movements. We have suggested classes of movements for the identification of the mass and of the general inertia properties of a held object. (S. Bitzer and S.Vijayakumar (2009), Latent Spaces for Dynamic Movement Primitives, Proc. 9th IEEE RAS International Conference on humanoid Robots (Humanoids \x9209), Paris, France.)
In addition, we investigated ways to actively extract information from sensory data by using appropriate exploratory movements. For active learning, we are interested in determining the optimal action x* to take during test time such that the Mutual Information between sensors y and hidden latent state θ, I(θ; y | x), is maximized.
This framework was successfully implemented in the framework of Gaussian Process sensor action modelling and Quadratic Mutual Information (QMI) based action selection (Saal HP, Ting J, Vijayakumar S (2010a). Active sequential learning with tactile feedback. Proc. Int. Conf. on Artificial Intelligence and Statistics (AISTATS) 2010; Saal HP, Ting J, Vijayakumar S (2010b). Active Estimation of Object Dynamics with Tactile Sensors. Proc. IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS 2010)). This theoretically well founded formulation was implemented with excellent results on the tactile discrimination of liquid viscosities in real time on a Schunk tactile hand.
|
|

